About the CoMSES Model Library more info
Our mission is to help computational modelers develop, document, and share their computational models in accordance with community standards and good open science and software engineering practices. Model authors can publish their model source code in the Computational Model Library with narrative documentation as well as metadata that supports open science and emerging norms that facilitate software citation, computational reproducibility / frictionless reuse, and interoperability. Model authors can also request private peer review of their computational models. Models that pass peer review receive a DOI once published.
All users of models published in the library must cite model authors when they use and benefit from their code.
Please check out our model publishing tutorial and feel free to contact us if you have any questions or concerns about publishing your model(s) in the Computational Model Library.
We also maintain a curated database of over 7500 publications of agent-based and individual based models with detailed metadata on availability of code and bibliometric information on the landscape of ABM/IBM publications that we welcome you to explore.
Displaying 10 of 11 results homophily clear search
Peer reviewed The effect of homophily on co-offending outcomes
Ruslan Klymentiev Christophe Vandeviver Luis E. C. Rocha | Published Friday, September 26, 2025This Agent-Based Model is designed to simulate how similarity-based partner selection (homophily) shapes the formation of co-offending networks and the diffusion of skills within those networks. Its purpose is to isolate and test the effects of offenders’ preference for similar partners on network structure and information flow, under controlled conditions.
In the model, offenders are represented as agents with an individual attribute and a set of skills. At each time step, agents attempt to select partners based on similarity preference. When two agents mutually select each other, they commit a co-offense, forming a tie and exchanging a skill. The model tracks the evolution of network properties (e.g., density, clustering, and tie strength) as well as the spread of skills over time.
This simple and theoretical model does not aim to produce precise empirical predictions but rather to generate insights and test hypotheses about the trade-off between network stability and information diffusion. It provides a flexible framework for exploring how changes in partner selection preferences may lead to differences in criminal network dynamics. Although the model was developed to simulate offenders’ interactions, in principle, it could be applied to other social processes involving social learning and skills exchange.
…
Netlogo model ` Effect of Network Homophily and Partisanship on Social Media to “Oil Spill” Polarizations’
takuya nagura | Published Saturday, September 13, 2025This model was utilized for the simulation in the paper titled Effect of Network Homophily and Partisanship on Social Media to “Oil Spill” Polarizations. It allows you to examine whether oil spill polarization occurs through people’s communication under various conditions.
・Choose the network construction conditions you’d like to examine from the “rewire-style” chooser box.
・Select the desired strength of partisanship from the “partisanlevel” chooser box. You can also set the strength manually in the code tab.
・You can set the number of dynamic topics using the “number-of-topics” slider.
・Use the “divers-of-opinion” slider to set the number of preference types for each dynamic topic.
…
Agent-based model of team decision-making in hidden profile situations
Andreas Flache Jonas Stein Vincenz Frey | Published Thursday, April 20, 2023 | Last modified Friday, November 17, 2023The model presented here is extensively described in the paper ‘Talk less to strangers: How homophily can improve collective decision-making in diverse teams’ (forthcoming at JASSS). A full replication package reproducing all results presented in the paper is accessible at https://osf.io/76hfm/.
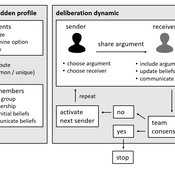
Narrative documentation includes a detailed description of the model, including a schematic figure and an extensive representation of the model in pseudocode.
The model develops a formal representation of a diverse work team facing a decision problem as implemented in the experimental setup of the hidden-profile paradigm. We implement a setup where a group seeks to identify the best out of a set of possible decision options. Individuals are equipped with different pieces of information that need to be combined to identify the best option. To this end, we assume a team of N agents. Each agent belongs to one of M groups where each group consists of agents who share a common identity.
The virtual teams in our model face a decision problem, in that the best option out of a set of J discrete options needs to be identified. Every team member forms her own belief about which decision option is best but is open to influence by other team members. Influence is implemented as a sequence of communication events. Agents choose an interaction partner according to homophily h and take turns in sharing an argument with an interaction partner. Every time an argument is emitted, the recipient updates her beliefs and tells her team what option she currently believes to be best. This influence process continues until all agents prefer the same option. This option is the team’s decision.
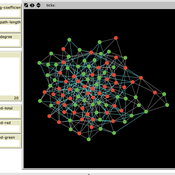
Two agent-based models of cooperation in dynamic groups and fixed social networks
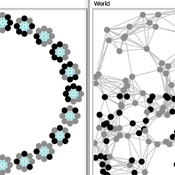
Carlos A. de Matos Fernandes | Published Thursday, January 20, 2022Both models simulate n-person prisoner dilemma in groups (left figure) where agents decide to C/D – using a stochastic threshold algorithm with reinforcement learning components. We model fixed (single group ABM) and dynamic groups (bad-barrels ABM). The purpose of the bad-barrels model is to assess the impact of information during meritocratic matching. In the bad-barrels model, we incorporated a multidimensional structure in which agents are also embedded in a social network (2-person PD). We modeled a random and homophilous network via a random spatial graph algorithm (right figure).
Peer reviewed OfficeMoves: Personalities and Performance in an Interdependent Environment
Alan Dugger | Published Thursday, June 11, 2020After a little work experience, we realize that different kinds of people prefer different work environments: some enjoy a fast-paced challenge; some want to get by; and, others want to show off.
From that experience, we also realize that different kinds of people affect their work environments differently: some increase the pace; some slow it down; and, others make it about themselves.
This model concerns how three different kinds of people affect their work environment and how that work environment affects them in return. The model explores how this circular relation between people’s preferences and their environment creates patterns of association and performance over time.
…
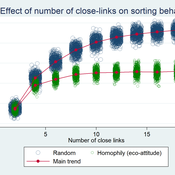
Waste separation in small-world networks
František Kalvas Michaela Kudrnáčová | Published Monday, September 30, 2019The model answers the question how homophily and number of close-links in small-world network influences behavior of consumats. The results show that the more close-links the more probable the consumat follows the major behavior, but homophilly blocks the major behavior and supports survival of the minor behavior.
Homophily as a process generating social networks: insights from Social Distance Attachment model
Szymon Talaga Andrzej Nowak | Published Tuesday, September 17, 2019This is code repository for the paper “Homophily as a process generating social networks: insights from Social Distance Attachment model”.
It provides all information, code and data necessary to replicate all the simulations and analyses presented in the paper.
This document contains the overall instruction as well as description of the content of the repository.
Details regarding particular stages are documented within source files as comments.
Homophily-driven Network Evolution and Diffusion
Gönenç Yücel Mustafa Yavaş | Published Thursday, January 08, 2015The model is an experimental ground to study the impact of network structure on diffusion. It allows to construct a social network that already has some measurable level of homophily, and simulate a diffusion process over this social network.
DITCH --- A Model of Inter-Ethnic Partnership Formation
Ruth Meyer Laurence Lessard-Phillips Huw Vasey | Published Wednesday, November 05, 2014 | Last modified Tuesday, February 02, 2016The DITCH model has been developed to investigate partner selection processes, focusing on individual preferences, opportunities for contact, and group size to uncover how these may lead to differential rates of inter-ethnic marriage.
Homophily and Distance Depending Network Generation for Modelling Opinion Dynamics
Sascha Holzhauer | Published Wednesday, August 22, 2012 | Last modified Tuesday, June 18, 2013The model uses opinion dynamics to test a simple and ecient but empirically based approach for generating social networks in spatial agent-based models which explicitly takes into account restrictions and opportunities imposed by effects of baseline homophily and considers the probability of links that depends on geographical distance between potential partners.
Displaying 10 of 11 results homophily clear search