About the CoMSES Model Library more info
Our mission is to help computational modelers develop, document, and share their computational models in accordance with community standards and good open science and software engineering practices. Model authors can publish their model source code in the Computational Model Library with narrative documentation as well as metadata that supports open science and emerging norms that facilitate software citation, computational reproducibility / frictionless reuse, and interoperability. Model authors can also request private peer review of their computational models. Models that pass peer review receive a DOI once published.
All users of models published in the library must cite model authors when they use and benefit from their code.
Please check out our model publishing tutorial and feel free to contact us if you have any questions or concerns about publishing your model(s) in the Computational Model Library.
We also maintain a curated database of over 7500 publications of agent-based and individual based models with detailed metadata on availability of code and bibliometric information on the landscape of ABM/IBM publications that we welcome you to explore.
Displaying 10 of 184 results for "Nuno R Barros De Oliveira" clear search
MCR Model
Davide Secchi Nuno R Barros De Oliveira | Published Friday, July 22, 2016 | Last modified Saturday, January 23, 2021The aim of the model is to define when researcher’s assumptions of dependence or independence of cases in multiple case study research affect the results — hence, the understanding of these cases.
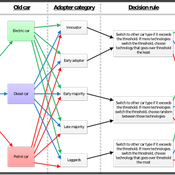
BESTMAP-ABM-DE is an agent-based model to determine the adoption and spatial allocation of selected agri-environmental schemes (AES) by individual farmers in the Mulde River Basin located in Western Saxony, Germany. The selected AES are buffer areas, cover crops, maintaining permanent grassland and conversion of arable land to permanent grassland. While the first three schemes have already been offered in the case study area, the latter scheme is a hypothetical scheme designed to test the impact of potential policy changes. For the first model analyses, only the currently offered schemes are considered. With the model, the effect of different scenarios of policy design on patterns of adoption can be investigated. In particular, the model can be used to study the social-ecological consequences of agricultural policies at different spatial and temporal scales and, in combination with biophysical models, test the ecological implications of different designs of the EU’s Common Agricultural Policy. The model was developed in the BESTMAP project.
Vacunación-Covid Ecuador
Adrian Lara | Published Tuesday, March 22, 2022El modelo a continuación, fue desarrollado para el DATA CHALLENGE 2022. Es un análisis de la información descargada del Portal de datos abiertos de Ecuador. Dentro del modelo podemos realizar una breve exploración de la información así como una simulación respecto al proceso de vacunación en Ecuador.
(De-)Stabilising effect of diffusions
Julia Kasmire Bert Van Meeuwen Cornelis Eikelboom | Published Tuesday, August 11, 2015What is stable: the large but coordinated change during a diffusion or the small but constant and uncoordinated changes during a dynamic equilibrium? This agent-based model of a diffusion creates output that reveal insights for system stability.
Peer reviewed Reduced Mobility Transition Model (R-MoTMo)
Gesine A. Steudle Sarah Wolf Steffen Fürst | Published Tuesday, December 06, 2022The Mobility Transition Model (MoTMo) is a large scale agent-based model to simulate the private mobility demand in Germany until 2035. Here, we publish a very much reduced version of this model (R-MoTMo) which is designed to demonstrate the basic modelling ideas; the aim is by abstracting from the (empirical, technological, geographical, etc.) details to examine the feed-backs of individual decisions on the socio-technical system.
A Mathematical Model of The Beer Game
Hakan Yasarcan Mert Edali | Published Wednesday, November 05, 2014This is the R code of the mathematical model that includes the decision making formulations for artificial agents. This code corresponds to equations 1-70 given in the paper “A Mathematical Model of The Beer Game”.
This is the R code of the mathematical model that includes the decision making formulations for artificial agents. Plus, the code for graphical output is also added to the original code.
A Mathematical Model of The Beer Game Coded in R for Verification
Hakan Yasarcan Mert Edali | Published Wednesday, November 05, 2014This is the R code of the mathematical model used for verification. This code corresponds to equations 1-9, 15-53, 58-62, 69-70, and 72-75 given in the paper “A Mathematical Model of The Beer Game”.
BEEHAVE Extension: Varroa mite control within Good Beekeeping Practice in Germany
Volker Grimm Jürgen Groeneveld Isabel Schödl | Published Wednesday, May 25, 2022 | Last modified Monday, November 07, 2022The western honey bee Apis mellifera is the most important pollinator in the world. The biggest threat to managed honey bees is the ectoparasitic mite Varroa destructor and the viruses DWV (Deformed Wing Virus) and APV (Acute Paralysis Virus) it transmits. Untreated honey bee colonies are expected to die within one to three years. This led to the development of strategies for beekeepers to control the Varroa mite in honey bee colonies and ensure the health and survival of their bee colonies, so called Good Beekeeping Practice. The aim of the extension of BEEHAVE was to represent the Good Beekeeping Practice of Varroa control in Germany. The relevant measures within the Varroa control strategies are drone brood removal as a Varroa trap and the treatment of bee colonies with organic acaricides (formic and oxalic acid) to kill the mites. This extension improves BEEHAVE and builds a bridge between beekeepers in practice and in the modelling world. It vastly contributes to the future use of BEEHAVE in beekeeping education in Germany.
Two agent-based models of cooperation in dynamic groups and fixed social networks
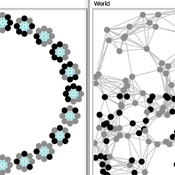
Carlos A. de Matos Fernandes | Published Thursday, January 20, 2022Both models simulate n-person prisoner dilemma in groups (left figure) where agents decide to C/D – using a stochastic threshold algorithm with reinforcement learning components. We model fixed (single group ABM) and dynamic groups (bad-barrels ABM). The purpose of the bad-barrels model is to assess the impact of information during meritocratic matching. In the bad-barrels model, we incorporated a multidimensional structure in which agents are also embedded in a social network (2-person PD). We modeled a random and homophilous network via a random spatial graph algorithm (right figure).
Displaying 10 of 184 results for "Nuno R Barros De Oliveira" clear search