This model grows land use patterns that emerge as a result of land-use compatibilities stablished in urban development plans, land topography, and street networks. It contains urban brushes to paint streets and land uses as a way to learn about urban pattern emergence through free experimentation.

The Village Project is designed to help archaeologists understand the factors influencing settlement patterns of small-scale agrarian peoples. Although such societies are becoming increasingly rare, they represent the norm throughout most of the Neolithic period the world over.

CoDMER v. 2.0 was parameterized with ethnographic data from organizations dealing with prescribed fire and seeding native plants, to advance theory on how collective decisions emerge in ecological restoration.

Reconstruction of the original code M. Cohen, J. March, and J. Olsen garbage can model, realized by means of Microsoft Office Excel 2010

Objective of our model is to simulate the emergence and operation of a technological niches (TN) in terms of actors’ interaction. A TN can be conceived as protected socio-economic space where radical innovations are developed and tested

This is a social trust model for investigating the social relationships and social networks in the real world and in social media.

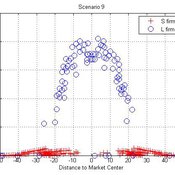
This model simulates the emergence of a dual market structure from firm-level interaction. Firms are profit-seeking, and demand is represented by a unimodal distribution of consumers along a set of taste positions.

The Relation-Based Model (RBM) purpose is to operationalise (a form of) process-relational (PR) thinking to serve as a thinking tool for process-relational thinking among social-ecological system (SES) researchers. The development of this model itself has been a ‘Proof of concept’- exercise to see whether we actually represent process-relational thinking in a methodology that is entity-based (ABM).

The target of the agent-based model is to show the emergence, change and disappearance of fishing assemblages (focusing on processes of self-organisation) in a Mexican fishery using a process-relational view. From this view, a fishery is regarded as an assemblage in which fishing can be enabled, fishing can occur, and fish can be bought/sold. These core doings - or sub-assemblages or capacities - maintain the assemblage. Each (sub)assemblage reflects different actualisations of constellations of relations and elements (buyers, fishers, fuel, permits, vessels and wind). The RBM thereby reflects an artificial fishery in which agents (elements) and their links (relations) engage in (enabling) fishing and buying/selling.

Hybrid attacks coordinate the exploitation of vulnerabilities across domains to undermine trust in authorities and cause social unrest. Whilst such attacks have primarily been seen in active conflict zones, there is growing concern about the potential harm that can be caused by hybrid attacks more generally and a desire to discover how better to identify and react to them. In addressing such threats, it is important to be able to identify and understand an adversary’s behaviour. Game theory is the approach predominantly used in security and defence literature for this purpose. However, the underlying rationality assumption, the equilibrium concept of game theory, as well as the need to make simplifying assumptions can limit its use in the study of emerging threats. To study hybrid threats, we present a novel agent-based model in which, for the first time, agents use reinforcement learning to inform their decisions. This model allows us to investigate the behavioural strategies of threat agents with hybrid attack capabilities as well as their broader impact on the behaviours and opinions of other agents.

This generic model simulates climate change adaptation in the form of resistance, accommodation, and retreat in coastal regions vulnerable to sea level rise and flooding. It tracks how population changes as households retreat to higher ground.