About the CoMSES Model Library more info
Our mission is to help computational modelers develop, document, and share their computational models in accordance with community standards and good open science and software engineering practices. Model authors can publish their model source code in the Computational Model Library with narrative documentation as well as metadata that supports open science and emerging norms that facilitate software citation, computational reproducibility / frictionless reuse, and interoperability. Model authors can also request private peer review of their computational models. Models that pass peer review receive a DOI once published.
All users of models published in the library must cite model authors when they use and benefit from their code.
Please check out our model publishing tutorial and feel free to contact us if you have any questions or concerns about publishing your model(s) in the Computational Model Library.
We also maintain a curated database of over 7500 publications of agent-based and individual based models with detailed metadata on availability of code and bibliometric information on the landscape of ABM/IBM publications that we welcome you to explore.
Displaying 10 of 293 results for "William J. Berger" clear search
Peer reviewed NetLogo model of USA mass shootings
Smarzhevskiy Ivan | Published Tuesday, September 24, 2019 | Last modified Tuesday, April 14, 2020Is the mass shooter a maniac or a relatively normal person in a state of great stress? According to the FBI report (Silver, J., Simons, A., & Craun, S. (2018). A Study of the Pre-Attack Behaviors of Active Shooters in the United States Between 2000 – 2013. Federal Bureau of Investigation, U.S. Department of Justice,Washington, D.C. 20535.), only 25% of the active shooters were known to have been diagnosed by a mental health professional with a mental illness of any kind prior to the offense.
The main objects of the model are the humans and the guns. The main factors influencing behavior are the population size, the number of people with mental disabilities (“psycho” in the model terminology) per 100,000 population, the total number of weapons (“guns”) in the population, the availability of guns for humans, the intensity of stressors affecting humans and the threshold level of stress, upon reaching which a person commits an act of mass shooting.
The key difference (in the model) between a normal person and a psycho is that a psycho accumulates stressors and, upon reaching a threshold level, commits an act of mass shooting. A normal person is exposed to stressors, but reaching the threshold level for killing occurs only when the simultaneous effect of stressors on him exceeds this level.
The population dynamics are determined by the following factors: average (normally distributed) life expectancy (“life_span” attribute of humans) and population growth with the percentage of newborns set by the value of the TickReprRatio% slider of the current population volume from 16 to 45 years old.Thus, one step of model time corresponds to a year.
Agent-based model of team decision-making in hidden profile situations
Andreas Flache Jonas Stein Vincenz Frey | Published Thursday, April 20, 2023 | Last modified Friday, November 17, 2023The model presented here is extensively described in the paper ‘Talk less to strangers: How homophily can improve collective decision-making in diverse teams’ (forthcoming at JASSS). A full replication package reproducing all results presented in the paper is accessible at https://osf.io/76hfm/.
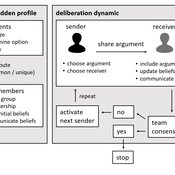
Narrative documentation includes a detailed description of the model, including a schematic figure and an extensive representation of the model in pseudocode.
The model develops a formal representation of a diverse work team facing a decision problem as implemented in the experimental setup of the hidden-profile paradigm. We implement a setup where a group seeks to identify the best out of a set of possible decision options. Individuals are equipped with different pieces of information that need to be combined to identify the best option. To this end, we assume a team of N agents. Each agent belongs to one of M groups where each group consists of agents who share a common identity.
The virtual teams in our model face a decision problem, in that the best option out of a set of J discrete options needs to be identified. Every team member forms her own belief about which decision option is best but is open to influence by other team members. Influence is implemented as a sequence of communication events. Agents choose an interaction partner according to homophily h and take turns in sharing an argument with an interaction partner. Every time an argument is emitted, the recipient updates her beliefs and tells her team what option she currently believes to be best. This influence process continues until all agents prefer the same option. This option is the team’s decision.
ForagerNet3_Demography: A Non-Spatial Model of Hunter-Gatherer Demography
Andrew White | Published Thursday, October 17, 2013 | Last modified Thursday, October 17, 2013ForagerNet3_Demography is a non-spatial ABM for exploring hunter-gatherer demography. Key methods represent birth, death, and marriage. The dependency ratio is an imporant variable in many economic decisions embedded in the methods.
ForagerNet3_Demography_V2
Andrew White | Published Thursday, February 13, 2014ForagerNet3_Demography_V2 is a non-spatial ABM for exploring hunter-gatherer demography. This version (developed from FN3D_V1) contains code for calculating the ratio of old to young adults (the “OY ratio”) in the living and dead populations.
Peer reviewed Emergent Firms Model
J M Applegate | Published Friday, July 13, 2018The Emergent Firm (EF) model is based on the premise that firms arise out of individuals choosing to work together to advantage themselves of the benefits of returns-to-scale and coordination. The Emergent Firm (EF) model is a new implementation and extension of Rob Axtell’s Endogenous Dynamics of Multi-Agent Firms model. Like the Axtell model, the EF model describes how economies, composed of firms, form and evolve out of the utility maximizing activity on the part of individual agents. The EF model includes a cash-in-advance constraint on agents changing employment, as well as a universal credit-creating lender to explore how costs and access to capital affect the emergent economy and its macroeconomic characteristics such as firm size distributions, wealth, debt, wages and productivity.
Peer reviewed General Housing Model
J M Applegate | Published Thursday, May 07, 2020The General Housing Model demonstrates a basic housing market with bank lending, renters, owners and landlords. This model was developed as a base to which students contributed additional functions during Arizona State University’s 2020 Winter School: Agent-Based Modeling of Social-Ecological Systems.
Peer reviewed Virus Transmission with Super-spreaders
J M Applegate | Published Saturday, September 11, 2021A curious aspect of the Covid-19 pandemic is the clustering of outbreaks. Evidence suggests that 80\% of people who contract the virus are infected by only 19% of infected individuals, and that the majority of infected individuals faile to infect another person. Thus, the dispersion of a contagion, $k$, may be of more use in understanding the spread of Covid-19 than the reproduction number, R0.
The Virus Transmission with Super-spreaders model, written in NetLogo, is an adaptation of the canonical Virus Transmission on a Network model and allows the exploration of various mitigation protocols such as testing and quarantines with both homogenous transmission and heterogenous transmission.
The model consists of a population of individuals arranged in a network, where both population and network degree are tunable. At the start of the simulation, a subset of the population is initially infected. As the model runs, infected individuals will infect neighboring susceptible individuals according to either homogenous or heterogenous transmission, where heterogenous transmission models super-spreaders. In this case, k is described as the percentage of super-spreaders in the population and the differing transmission rates for super-spreaders and non super-spreaders. Infected individuals either recover, at which point they become resistant to infection, or die. Testing regimes cause discovered infected individuals to quarantine for a period of time.
Peer reviewed Modern Wage Dynamics
J M Applegate | Published Sunday, June 05, 2022The Modern Wage Dynamics Model is a generative model of coupled economic production and allocation systems. Each simulation describes a series of interactions between a single aggregate firm and a set of households through both labour and goods markets. The firm produces a representative consumption good using labour provided by the households, who in turn purchase these goods as desired using wages earned, thus the coupling.
Each model iteration the firm decides wage, price and labour hours requested. Given price and wage, households decide hours worked based on their utility function for leisure and consumption. A labour market construct chooses the minimum of hours required and aggregate hours supplied. The firm then uses these inputs to produce goods. Given the hours actually worked, the households decide actual consumption and a market chooses the minimum of goods supplied and aggregate demand. The firm uses information gained through observing market transactions about consumption demand to refine their conceptions of the population’s demand.
The purpose of this model is to explore the general behaviour of an economy with coupled production and allocation systems, as well as to explore the effects of various policies on wage and production, such as minimum wage, tax credits, unemployment benefits, and universal income.
…
PFS - Preference Falsification Simulation (PreFalSim)
Francisco J Miguel Francisco J. León-Medina Jordi Tena-Sanchez | Published Monday, July 01, 2019A model for simulating the evolution of individual’s preferences, incliding adaptive agents “falsifying” -as public opinions- their own preferences. It was builded to describe, explore, experiment and understand how simple heuristics can modulate global opinion dynamics. So far two mechanisms are implemented: a version of Festiguer’s reduction of cognitive disonance, and a version of Goffman’s impression management. In certain social contexts -minority, social rank presure- some models agents can “fake” its public opinion while keeping internally the oposite preference, but after a number of rounds following this falsifying behaviour pattern, a coherence principle can change the real or internal preferences close to that expressed in public.
Carington
William Kennedy Emily S Ihara Catherine J Tompkins Michael E Wolf-Branigin | Published Thursday, July 13, 2017The Carington model is designed to provide insights into the factors affecting informal health care for older adults. It encompasses older adults, caregivers, and factors affecting informal health care. The Carington model includes no submodels.
Displaying 10 of 293 results for "William J. Berger" clear search