About the CoMSES Model Library more info
Our mission is to help computational modelers develop, document, and share their computational models in accordance with community standards and good open science and software engineering practices. Model authors can publish their model source code in the Computational Model Library with narrative documentation as well as metadata that supports open science and emerging norms that facilitate software citation, computational reproducibility / frictionless reuse, and interoperability. Model authors can also request private peer review of their computational models. Models that pass peer review receive a DOI once published.
All users of models published in the library must cite model authors when they use and benefit from their code.
Please check out our model publishing tutorial and feel free to contact us if you have any questions or concerns about publishing your model(s) in the Computational Model Library.
We also maintain a curated database of over 7500 publications of agent-based and individual based models with detailed metadata on availability of code and bibliometric information on the landscape of ABM/IBM publications that we welcome you to explore.
Displaying 10 of 359 results for "John C Moore" clear search
Residents planned behaviour of waste sorting to explore urban situations
Jonathan Edgardo Cohen | Published Wednesday, June 07, 2023 | Last modified Thursday, March 14, 2024Municipal waste management (MWM) is essential for urban development. Efficient waste management is essential for providing a healthy and clean environment, for reducing GHGs and for increasing the amount of material recycled. Waste separation at source is perceived as an effective MWM strategy that relays on the behaviour of citizens to separate their waste in different fractions. The strategy is straightforward, and many cities have adopted the strategy or are working to implement it. However, the success of such strategy depends on adequate understanding of the drivers of the behaviour of proper waste sorting. The Theory of Planned Behaviour (TPB) has been extensively applied to explain the behaviour of waste sorting and contributes to determining the importance of different psychological constructs. Although, evidence shows its validity in different contexts, without exploring how urban policies and the built environment affect the TPB, its application to urban challenges remains unlocked. To date, limited research has focused in exposing how different urban situations such as: distance to waste bins, conditions of recycling facilities or information campaigns affect the planned behaviour of waste separation. To fill this gap, an agent-based model (ABM) of residents capable of planning the behaviour of waste separation is developed. The study is a proof of concept that shows how the TPB can be combined with simulations to provide useful insights to evaluate different urban planning situations. In this paper we depart from a survey to capture TPB constructs, then Structural Equation Modelling (SEM) is used to validate the TPB hypothesis and extract the drivers of the behaviour of waste sorting. Finally, the development of the ABM is detailed and the drivers of the TPB are used to determine how the residents behave. A low-density and a high-density urban scenario are used to extract policy insights. In conclusion, the integration between the TPB into ABMs can help to bridge the knowledge gap between can provide a useful insight to analysing and evaluating waste management scenarios in urban areas. By better understanding individual waste sorting behaviour, we can develop more effective policies and interventions to promote sustainable waste management practices.
Peer reviewed AMRO_CULEX_WNV
Aniruddha Belsare Jennifer Owen | Published Saturday, February 27, 2021 | Last modified Thursday, March 11, 2021An agent-based model simulating West Nile Virus dynamics in a one host (American robin)-one vector (Culex spp. mosquito) system. ODD improved and code cleaned.
Formal Organization Hierarchy and Informal Networks - "The Company Behind the Org Chart"
Tom Briggs | Published Sunday, April 18, 2021A generalized organizational agent- based model (ABM) containing both formal organizational hierarchy and informal social networks simulates organizational processes that occur over both formal network ties and informal networks.
Narragansett Bay (RI) Recreational Fishery ABM
Tyler Pavlowich Anne Innes-Gold Margaret Heinichen M. Conor McManus Jason McNamee Jeremy Collie Austin Humphries | Published Monday, June 21, 2021This model is based on the Narragansett Bay, RI recreational fishery. The two types of agents are piscivorous fish and fishers (shore and boat fishers are separate “breeds”). Each time step represents one week. Open season is weeks 1-26, assuming fishing occurs during half the year. At each weekly time step, fish agents grow, reproduce, and die. Fisher agents decide whether or not to fish based on their current satisfaction level, and those that do go fishing attempt to catch a fish. If they are successful, they decide whether to keep or release the fish. In our publication, this model was linked to an Ecopath with Ecosim food web model where the commercial harvest of forage fish affected the biomass of piscivorous fish - which then became the starting number of piscivorous fish for this ABM. The number of fish caught in a season of this ABM was converted to a fishing pressure and input back into the food web model.
Peer reviewed Coupled demographic dynamics of herd and household in pastoral systems
Mark Moritz Ian M Hamilton Andrew Yoak Abigail Buffington Chelsea E Hunter Daniel C Peart | Published Saturday, April 08, 2023This purpose of this model is to understand how the coupled demographic dynamics of herds and households constrain the growth of livestock populations in pastoral systems.
NarrABS
Tilman Schenk | Published Thursday, September 20, 2012 | Last modified Saturday, April 27, 2013An agent based simulation of a political process based on stakeholder narratives
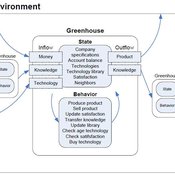
Universal Darwinism in Dutch Greenhouses
Julia Kasmire | Published Wednesday, May 09, 2012 | Last modified Saturday, April 27, 2013An ABM, derived from a case study and a series of surveys with greenhouse growers in the Westland, Netherlands. Experiments using this model showshow that the greenhouse horticulture industry displays diversity, adaptive complexity and an uneven distribution, which all suggest that the industry is an evolving system.
Collective Decision Making for Ecological Restoration version 2.0
Dean Massey Moira Zellner Cristy Watkins Jeremy Brooks Kristen Ross Lynne M Westphal | Published Wednesday, November 19, 2014CoDMER v. 2.0 was parameterized with ethnographic data from organizations dealing with prescribed fire and seeding native plants, to advance theory on how collective decisions emerge in ecological restoration.
Kulayinjana
Christophe Le Page Arthur Perrotton Michel De Garine-Wichatitsky Barry Bitu Killion Koyisi Ferdinand Mwamba Cephus Ncube Victor Ncube Siphusisiwe Ndlovu Raphael Ngwenya Ambu Nyathi Fumbane Nyathi Patrick Sibanda Zenzo Sibanda | Published Monday, October 03, 2016a computer-based role-playing game simulating the interactions between farming activities, livestock herding and wildlife in a virtual landscape reproducing local socioecological dynamics at the periphery of Hwange National Park (Zimbabwe).
Peer reviewed HUMLAND FIRE-IN-THE-HOLE agent-based model
Fulco Scherjon Anastasia Nikulina | Published Monday, October 20, 2025HUMLAND Fire-in-the-Hole is a conceptual agent-based model (ABM) designed to explore the ecological and behavioral consequences of fire-driven hunting strategies employed by hunter-gatherers, specifically Neanderthals, during the Last Interglacial period around the Neumark-Nord (Germany) archaeological site.
This model builds on and specializes the HUMLAND 1.0.0 model (Nikulina et al. 2024), integrating anthropogenic fires, elephant group behavior, and landscape response to simulate interactions between humans, megafauna, and vegetation over time.
Displaying 10 of 359 results for "John C Moore" clear search