The NIER model is intended to add qualitative variables of building owner types and peer group scales to existing energy efficiency retrofit adoption models. The model was developed through a combined methodology with qualitative research, which included interviews with key stakeholders in Cleveland, Ohio and Detroit and Grand Rapids, Michigan. The concepts that the NIER model adds to traditional economic feasibility studies of energy retrofit decision-making are differences in building owner types (reflecting strategies for managing buildings) and peer group scale (neighborhoods of various sizes and large-scale Districts). Insights from the NIER model include: large peer group comparisons can quickly raise the average energy efficiency values of Leader and Conformist building owner types, but leave Stigma-avoider owner types as unmotivated to retrofit; policy interventions such as upgrading buildings to energy-related codes at the point of sale can motivate retrofits among the lowest efficient buildings, which are predominantly represented by the Stigma-avoider type of owner; small neighborhood peer groups can successfully amplify normal retrofit incentives.

This model is an extension of the Artificial Long House Valley (ALHV) model developed by the authors (Swedlund et al. 2016; Warren and Sattenspiel 2020). The ALHV model simulates the population dynamics of individuals within the Long House Valley of Arizona from AD 800 to 1350. Individuals are aggregated into households that participate in annual agricultural and demographic cycles. The present version of the model incorporates features of the ALHV model including realistic age-specific fertility and mortality and, in addition, it adds the Black Mesa environment and population, as well as additional methods to allow migration between the two regions.

As is the case for previous versions of the ALHV model as well as the Artificial Anasazi (AA) model from which the ALHV model was derived (Axtell et al. 2002; Janssen 2009), this version makes use of detailed archaeological and paleoenvironmental data from the Long House Valley and the adjacent areas in Arizona. It also uses the same methods as the original AA model to estimate annual maize productivity of various agricultural zones within the Long House Valley. A new environment and associated methods have been developed for Black Mesa. Productivity estimates from both regions are used to determine suitable locations for households and farms during each year of the simulation.

This model represents an agent-based social simulation for citizenship competences. In this model people interact by solving different conflicts and a conflict is solved or not considering two possible escenarios: when individual citizenship competences are considered and when not. In both cases the TKI conflict resolution styles are considered. Each conflict has associated a competence and the information about the conflicts and their competences is retrieved from an ontology which was developed in Protégé. To do so, a NetLogo extension was developed using the Java programming language and the JENA API (to make queries over the ontology).

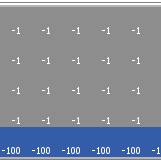
This model implements a classic scenario used in Reinforcement Learning problem, the “Cliff Walking Problem”. Consider the gridworld shown below (SUTTON; BARTO, 2018). This is a standard undiscounted, episodic task, with start and goal states, and the usual actions causing movement up, down, right, and left. Reward is -1 on all transitions except those into the region marked “The Cliff.” Stepping into this region incurs a reward of -100 and sends the agent instantly back to the start (SUTTON; BARTO, 2018).

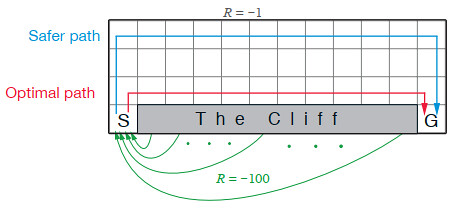
The problem is solved in this model using the Q-Learning algorithm. The algorithm is implemented with the support of the NetLogo Q-Learning Extension

This is a re-implementation of a the NetLogo model Maze (ROOP, 2006).

This re-implementation makes use of the Q-Learning NetLogo Extension to implement the Q-Learning, which is done only with NetLogo native code in the original implementation.

Extension of Pluchino et al.’s 2018 success vs talent model, to allow talented individuals to mitigate unlucky events.

This model is an extended version of the original MERCURY model (https://www.comses.net/codebases/4347/releases/1.1.0/ ) . It allows for experiments to be performed in which empirically informed population sizes of sites are included, that allow for the scaling of the number of tableware traders with the population of settlements, and for hypothesised production centres of four tablewares to be used in experiments.

Experiments performed with this population extension and substantive interpretations derived from them are published in:

Hanson, J.W. & T. Brughmans. In press. Settlement scale and economic networks in the Roman Empire, in T. Brughmans & A.I. Wilson (ed.) Simulating Roman Economies. Theories, Methods and Computational Models. Oxford: Oxford University Press.

…

A draft model with some useful code for creating different network structures using the Netlogo NW extension. This model is used for the following tutorial:
Brughmans, T. (2018). Network structures and assembling code in Netlogo, Tutorial, https://archaeologicalnetworks.wordpress.com/resources/#structures .

This is extended version of the MERCRUY model (Brughmans 2015) incorporates a ‘transport-cost’ variable, and is otherwise unchanged. This extended model is described in this publication: Brughmans, T., 2019. Evaluating the potential of computational modelling for informing debates on Roman economic integration, in: Verboven, K., Poblome, J. (Eds.), Structural Determinants in the Roman World.

Brughmans, T., 2015. MERCURY: an ABM of tableware trade in the Roman East. CoMSES Comput. Model Libr. URL https://www.comses.net/codebases/4347/releases/1.1.0/

The Emergent Firm (EF) model is based on the premise that firms arise out of individuals choosing to work together to advantage themselves of the benefits of returns-to-scale and coordination. The Emergent Firm (EF) model is a new implementation and extension of Rob Axtell’s Endogenous Dynamics of Multi-Agent Firms model. Like the Axtell model, the EF model describes how economies, composed of firms, form and evolve out of the utility maximizing activity on the part of individual agents. The EF model includes a cash-in-advance constraint on agents changing employment, as well as a universal credit-creating lender to explore how costs and access to capital affect the emergent economy and its macroeconomic characteristics such as firm size distributions, wealth, debt, wages and productivity.