About the CoMSES Model Library more info
Our mission is to help computational modelers develop, document, and share their computational models in accordance with community standards and good open science and software engineering practices. Model authors can publish their model source code in the Computational Model Library with narrative documentation as well as metadata that supports open science and emerging norms that facilitate software citation, computational reproducibility / frictionless reuse, and interoperability. Model authors can also request private peer review of their computational models. Models that pass peer review receive a DOI once published.
All users of models published in the library must cite model authors when they use and benefit from their code.
Please check out our model publishing tutorial and feel free to contact us if you have any questions or concerns about publishing your model(s) in the Computational Model Library.
We also maintain a curated database of over 7500 publications of agent-based and individual based models with detailed metadata on availability of code and bibliometric information on the landscape of ABM/IBM publications that we welcome you to explore.
Displaying 10 of 251 results for "Alison Heppenstall" clear search
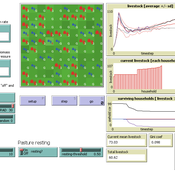
RAGE RAngeland Grazing Model
Carsten M Buchmann Jule Thober Birgit Müller Karin Frank Cheng Guo Jürgen Groeneveld Gunnar Dressler Niklas Hase | Published Monday, July 17, 2017 | Last modified Friday, October 26, 2018RAGE models a stylized common property grazing system. Agents follow a certain behavioral type. The model allows analyzing how household behavior with respect to a social norm on pasture resting affects long-term social-ecological system dynamics.
Telephone Game
Julia Kasmire | Published Friday, January 10, 2020This is a model of a game of Telephone (also known as Chinese Whishpers in the UK), with agents representing people that can be asked, to play. The first player selects a word from their internal vocabulary and “whispers” it to the next player, who may mishear it depending on the current noise level, who whispers that word to the next player, and so on.
When the game ends, the word chosen by the first player is compared to the word heard by the last player. If they match exactly, all players earn large prize. If the words do not match exactly, a small prize is awarded to all players for each part of the words that do match. Players change color to reflect their current prize-count. A histogram shows the distribution of colors over all the players.
The user can decide on factors like
* how many players there are,
…
Large-scale land acqusitions and smallholder food security
Tim Williams | Published Thursday, September 16, 2021Large-scale land acquisitions (LSLAs) threaten smallholder livelihoods globally. Despite more than a decade of research on the LSLA phenomenon, it remains a challenge to identify governance conditions that may foster beneficial outcomes for both smallholders and investors. One potentially promising strategy toward this end is contract farming (CF), which more directly involves smallholder households in commodity production than conditions of acquisition and displacement.
To improve understanding of how CF may mediate the outcomes of LSLAs, we developed an agent-based model of smallholder livelihoods, which we used as a virtual laboratory to experiment on a range of hypothetical LSLA and CF implementation scenarios.
The model represents a community of smallholder households in a mixed crop-livestock system. Each agent farms their own land and manages a herd of livestock. Agents can also engage in off-farm employment, for which they earn a fixed wage and compete for a limited number of jobs. The principal model outputs include measures of household food security (representing access to a single, staple food crop) and agricultural production (of a single, staple food crop).
…
00b SimEvo_V5.08 NetLogo
Garvin Boyle | Published Saturday, October 05, 2019In 1985 Dr Michael Palmiter, a high school teacher, first built a very innovative agent-based model called “Simulated Evolution” which he used for teaching the dynamics of evolution. In his model, students can see the visual effects of evolution as it proceeds right in front of their eyes. Using his schema, small linear changes in the agent’s genotype have an exponential effect on the agent’s phenotype. Natural selection therefore happens quickly and effectively. I have used his approach to managing the evolution of competing agents in a variety of models that I have used to study the fundamental dynamics of sustainable economic systems. For example, here is a brief list of some of my models that use “Palmiter Genes”:
- ModEco - Palmiter genes are used to encode negotiation strategies for setting prices;
- PSoup - Palmiter genes are used to control both motion and metabolic evolution;
- TpLab - Palmiter genes are used to study the evolution of belief systems;
- EffLab - Palmiter genes are used to study Jevon’s Paradox, EROI and other things.
…
Peer reviewed The Indus Village's Weather model: procedural generation of daily weather
Andreas Angourakis | Published Tuesday, May 13, 2025Overview
The Weather model is a procedural generation model designed to create realistic daily weather data for socioecological simulations. It generates synthetic weather time series for solar radiation, temperature, and precipitation using algorithms based on sinusoidal and double logistic functions. The model incorporates stochastic variation to mimic unpredictable weather patterns and aims to provide realistic yet flexible weather inputs for exploring diverse climate scenarios.
The Weather model can be used independently or integrated into larger models, providing realistic weather patterns without extensive coding or data collection. It can be customized to meet specific requirements, enabling users to gain a better understanding of the underlying mechanisms and have greater confidence in their applications.
…
The various technologies used inside a Dutch greenhouse interact in combination with an external climate, resulting in an emergent internal climate, which contributes to the final productivity of the greenhouse. This model examines how differing technology development styles affects the overall ability of a community of growers to approach the theoretical maximum yield.
Agent-based model for the socio-economic monitoring of visitor streams
Stefan Mohr | Published Saturday, January 20, 2018Due to the large extent of the Harz National Park, an accurate measurement of visitor numbers and their spatiotemporal distribution is not feasible. This model demonstrates the possibility to simulate the streams of visitors with ABM methodology.
How does knowledge infrastructure mobilization influence the safe operating space of regulated exploited ecosystems?
Jean-Denis Mathias | Published Tuesday, July 17, 2018Decision-makers often have to act before critical times to avoid the collapse of ecosystems using knowledge \textcolor{red}{that can be incomplete or biased}. Adaptive management may help managers tackle such issues. However, because the knowledge infrastructure required for adaptive management may be mobilized in several ways, we study the quality and the quantity of knowledge provided by this knowledge infrastructure. In order to analyze the influence of mobilized knowledge, we study how the following typology of knowledge and its use may impact the safe operating space of exploited ecosystems: 1) knowledge of the past based on a time series distorted by measurement errors; 2) knowledge of the current systems’ dynamics based on the representativeness of the decision-makers’ mental models of the exploited ecosystem; 3) knowledge of future events based on decision-makers’ likelihood estimates of extreme events based on modeling infrastructure (models and experts to interpret them) they have at their disposal. We consider different adaptive management strategies of a general regulated exploited ecosystem model and we characterize the robustness of these strategies to biased knowledge. Our results show that even with significant mobilized knowledge and optimal strategies, imperfect knowledge may still shrink the safe operating space of the system leading to the collapse of the system. However, and perhaps more interestingly, we also show that in some cases imperfect knowledge may unexpectedly increase the safe operating space by suggesting cautious strategies.
The code enables to calculate the safe operating spaces of different managers in the case of biased and unbiased knowledge.
Location Analysis Hybrid ABM
Lukasz Kowalski | Published Friday, February 08, 2019The purpose of this hybrid ABM is to answer the question: where is the best place for a new swimming pool in a region of Krakow (in Poland)?
The model is well described in ODD protocol, that can be found in the end of my article published in JASSS journal (available online: http://jasss.soc.surrey.ac.uk/22/1/1.html ). Comparison of this kind of models with spatial interaction ones, is presented in the article. Before developing the model for different purposes, area of interest or services, I recommend reading ODD protocol and the article.
I published two films on YouTube that present the model: https://www.youtube.com/watch?v=iFWG2Xv20Ss , https://www.youtube.com/watch?v=tDTtcscyTdI&t=1s
…
This model extends the original Artifical Anasazi (AA) model to include individual agents, who vary in age and sex, and are aggregated into households. This allows more realistic simulations of population dynamics within the Long House Valley of Arizona from AD 800 to 1350 than are possible in the original model. The parts of this model that are directly derived from the AA model are based on Janssen’s 1999 Netlogo implementation of the model; the code for all extensions and adaptations in the model described here (the Artificial Long House Valley (ALHV) model) have been written by the authors. The AA model included only ideal and homogeneous “individuals” who do not participate in the population processes (e.g., birth and death)–these processes were assumed to act on entire households only. The ALHV model incorporates actual individual agents and all demographic processes affect these individuals. Individuals are aggregated into households that participate in annual agricultural and demographic cycles. Thus, the ALHV model is a combination of individual processes (birth and death) and household-level processes (e.g., finding suitable agriculture plots).
As is the case for the AA model, the ALHV model makes use of detailed archaeological and paleoenvironmental data from the Long House Valley and the adjacent areas in Arizona. It also uses the same methods as the original model (from Janssen’s Netlogo implementation) to estimate annual maize productivity of various agricultural zones within the valley. These estimates are used to determine suitable locations for households and farms during each year of the simulation.
Displaying 10 of 251 results for "Alison Heppenstall" clear search