About the CoMSES Model Library more info
Our mission is to help computational modelers develop, document, and share their computational models in accordance with community standards and good open science and software engineering practices. Model authors can publish their model source code in the Computational Model Library with narrative documentation as well as metadata that supports open science and emerging norms that facilitate software citation, computational reproducibility / frictionless reuse, and interoperability. Model authors can also request private peer review of their computational models. Models that pass peer review receive a DOI once published.
All users of models published in the library must cite model authors when they use and benefit from their code.
Please check out our model publishing tutorial and feel free to contact us if you have any questions or concerns about publishing your model(s) in the Computational Model Library.
We also maintain a curated database of over 7500 publications of agent-based and individual based models with detailed metadata on availability of code and bibliometric information on the landscape of ABM/IBM publications that we welcome you to explore.
Displaying 10 of 113 results random clear search
Role of Diversity in Team Performance: the Case of Missing Expertise, an Agent Based Simulations
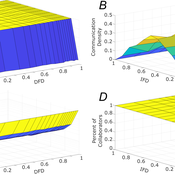
Tamás Kiss | Published Friday, December 29, 2023This ABM simulates problem solving agents as they work on a set of tasks. Each agent has a trait vector describing their skills. Two agents might form a collaboration if their traits are similar enough. Tasks are defined by a component vector. Agents work on tasks by decreasing tasks’ component vectors towards zero.
The simulation generates agents with given intrapersonal functional diversity (IFD), and dominant function diversity (DFD), and a set of random tasks and evaluates how agents’ traits influence their level of communication and the performance of a team of agents.
Modeling results highlight the importance of the distributions of agents’ properties forming a team, and suggests that for a thorough description of management teams, not only diversity measures based on individual agents, but an aggregate measure is also required.
…
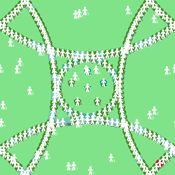
Peer reviewed A Bayesian Nash Equilibrium (BNE)-informed ABM for pedestrian evacuation in different constricted spaces
Jiaqi Ge Yiyu Wang Alexis Comber | Published Wednesday, October 11, 2023This BNE-informed ABM ultimately aims to provide a more realistic description of complicated pedestrian behaviours especially in high-density and life-threatening situations. Bayesian Nash Equilibrium (BNE) was adopted to reproduce interactive decision-making process among rational and game-playing agents. The implementations of 3 behavioural models, which are Shortest Route (SR) model, Random Follow (RF) model, and BNE model, make it possible to simulate emergent patterns of pedestrian behaviours (e.g. herding and self-organised queuing behaviours, etc.) in emergency situations.
According to the common features of previous mass trampling accidents, a series of simulation experiments were performed in space with 3 types of barriers, which are Horizontal Corridors, Vertical Corridors, and Random Squares, standing for corridors, bottlenecks and intersections respectively, to investigate emergent behaviours of evacuees in varied constricted spatial environments. The output of this ABM has been available at https://data.mendeley.com/datasets/9v4byyvgxh/1.
Correlated random walk (Javascript)
Viktoriia Radchuk Uta Berger Thibault Fronville | Published Tuesday, May 09, 2023The first simple movement models used unbiased and uncorrelated random walks (RW). In such models of movement, the direction of the movement is totally independent of the previous movement direction. In other words, at each time step the direction, in which an individual is moving is completely random. This process is referred to as a Brownian motion.
On the other hand, in correlated random walks (CRW) the choice of the movement directions depends on the direction of the previous movement. At each time step, the movement direction has a tendency to point in the same direction as the previous one. This movement model fits well observational movement data for many animal species.
The presented agent based model simulated the movement of the agents as a correlated random walk (CRW). The turning angle at each time step follows the Von Mises distribution with a ϰ of 10. The closer ϰ gets to zero, the closer the Von Mises distribution becomes uniform. The larger ϰ gets, the more the Von Mises distribution approaches a normal distribution concentrated around the mean (0°).
In this script the turning angles (following the Von Mises distribution) are generated based on the the instructions from N. I. Fisher 2011.
This model is implemented in Javascript and can be used as a building block for more complex agent based models that would rely on describing the movement of individuals with CRW.
Peer reviewed Correlated Random Walk (NetLogo)
Viktoriia Radchuk Uta Berger Thibault Fronville | Published Tuesday, May 09, 2023 | Last modified Monday, December 18, 2023This is NetLogo code that presents two alternative implementations of Correlated Random Walk (CRW):
- 1. drawing the turning angles from the uniform distribution, i.e. drawing the angle with the same probability from a certain given range;
- 2. drawing the turning angles from von Mises distribution.
The move lengths are drawn from the lognormal distribution with the specified parameters.
Correlated Random Walk is used to represent the movement of animal individuals in two-dimensional space. When modeled as CRW, the direction of movement at any time step is correlated with the direction of movement at the previous time step. Although originally used to describe the movement of insects, CRW was later shown to sufficiently well describe the empirical movement data of other animals, such as wild boars, caribous, sea stars.
…
Peer reviewed ArchMatNet: Archaeological Material Networks
Claudine Gravel-Miguel Robert Bischoff Cecilia Padilla-Iglesias | Published Monday, February 20, 2023The purpose of the model is to investigate how different factors affect the ability of researchers to reconstruct prehistoric social networks from artifact stylistic similarities, as well as the overall diversity of cultural traits observed in archaeological assemblages. Given that cultural transmission and evolution is affected by multiple interacting phenomena, our model allows to simultaneously explore six sets of factors that may condition how social networks relate to shared culture between individuals and groups:
- Factors relating to the structure of social groups
- Factors relating to the cultural traits in question
- Factors relating to individual learning strategies
- Factors relating to the environment
…
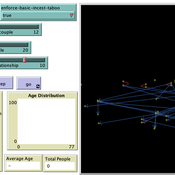
Peer reviewed Monogamous Reproduction in Small Populations and the Enforcement of the Incest Taboo
Ian Stuart | Published Wednesday, January 18, 2023This program was developed to simulate monogamous reproduction in small populations (and the enforcement of the incest taboo).
Every tick is a year. Adults can look for a mate and enter a relationship. Adult females in a Relationship (under the age of 52) have a chance to become pregnant. Everyone becomes not alive at 77 (at which point people are instead displayed as flowers).
User can select a starting-population. The starting population will be adults between the ages of 18 and 42.
…
Peer reviewed Personnel decisions in the hierarchy
Smarzhevskiy Ivan | Published Friday, August 19, 2022This is a model of organizational behavior in the hierarchy in which personnel decisions are made.
The idea of the model is that the hierarchy, busy with operations, is described by such characteristics as structure (number and interrelation of positions) and material, filling these positions (persons with their individual performance). A particular hierarchy is under certain external pressure (performance level requirement) and is characterized by the internal state of the material (the distribution of the perceptions of others over the ensemble of persons).
The World of the model is a four-level hierarchical structure, consisting of shuff positions of the top manager (zero level of the hierarchy), first-level managers who are subordinate to the top manager, second-level managers (subordinate to the first-level managers) and positions of employees (the third level of the hierarchy). ) subordinated to the second-level managers. Such a hierarchy is a tree, i.e. each position, with the exception of the position of top manager, has a single boss.
Agents in the model are persons occupying the specified positions, the number of persons is set by the slider (HumansQty). Personas have some operational performance (harisma, an unfortunate attribute name left over from the first edition of the model)) and a sense of other personas’ own perceptions. Performance values are distributed over the ensemble of persons according to the normal law with some mean value and variance.
The value of perception by agents of each other is positive or negative (implemented in the model as numerical values equal to +1 and -1). The distribution of perceptions over an ensemble of persons is implemented as a random variable specified by the probability of negative perception, the value of which is set by the control elements of the model interface. The numerical value of the probability equal to 0 corresponds to the case in which all persons positively perceive each other (the numerical value of the random variable is equal to 1, which corresponds to the positive perception of the other person by the individual).
The hierarchy is occupied with operational activity, the degree of intensity of which is set by the external parameter Difficulty. The level of productivity of each manager OAIndex is equal to the level of productivity of the department he leads and is the ratio of the sum of productivity of employees subordinate to the head to the level of complexity of the work Difficulty. An increase in the numerical value of Difficulty leads to a decrease in the OAIndex for all subdivisions of the hierarchy. The managerial meaning of the OAIndex indicator is the percentage of completion of the load specified for the hierarchy as a whole, i.e. the ratio of the actual performance of the structural subdivisions of the hierarchy to the required performance, the level of which is specified by the value of the Difficulty parameter.
…
Biodiversity and Adoption of Small-scale Agroforestry in Rwanda (BASAR)
Beatrice Nöldeke Etti Winter Elisée Bahati Ntawuhiganayo | Published Friday, July 15, 2022The BASAR model aims to investigate different approaches to describe small-scale farmers’ decision-making in the context of diversified agroforestry adoption in rural Rwanda. Thereby, it compares random behaviour with perfect rationality (non-discounted and discounted utility maximization), bounded rationality (satisficing and fast and frugal decision tree heuristics), Theory of Planned Behaviour, and a probabilistic regression-based approach. It is aimed at policy-makers, extension agents, and cooperatives to better understand how rural farmers decide about implementing innovative agricultural practices such as agroforestry and at modelers to support them in selecting an approach to represent human decision-making in ABMs of Social-Ecological Systems. The overall objective is to identify a suitable approach to describe human decision-making and therefore improve forecasts of adoption rates and support the development and implementation of interventions that aim to raise low adoption rates.
Peer reviewed An agent-based simulation model of pedestrian evacuation based on Bayesian Nash Equilibrium
Jiaqi Ge Yiyu Wang Alexis Comber | Published Wednesday, July 06, 2022This ABM aims to introduce a new individual decision-making model, BNE into the ABM of pedestrian evacuation to properly model individual behaviours and motions in emergency situations. Three types of behavioural models has been developed, which are Shortest Route (SR) model, Random Follow (RF) model, and BNE model, to better reproduce evacuation dynamics in a tunnel space. A series of simulation experiments were conducted to evaluate the simulating performance of the proposed ABM.
ABM for Underwater optical wireless communication in a water tank
Mohamed ABID | Published Sunday, May 29, 2022This model simulates the propagation of photons in a water tank. A source of light emits an impulse of photons with equal energy represented by yellow dots. These photons are then scattered by water particles before possibly reaching the photo-detector represented by a gray line. Different types of water are considered. For each one of them we calculate the total received energy.
The water tank is represented by a blue rectangle with fixed dimensions. It’s exposed to the air interface and has totally absorbent barriers. Four types of water are supported. Each one is characterized by its absorption and scattering coefficients.
At the source, the photons are generated uniformly with a random direction within the beamwidth. Each photon travels a random distance drawn from a distribution depending on the water characteristics before encountering a water particle.
Based on the updated position of the photon, three situations may occur:
-The photon hits the barrier of the tank on its trajectory. In this case it’s considered as lost since the barriers are assumed totally absorbent.
…
Displaying 10 of 113 results random clear search