About the CoMSES Model Library more info
Our mission is to help computational modelers develop, document, and share their computational models in accordance with community standards and good open science and software engineering practices. Model authors can publish their model source code in the Computational Model Library with narrative documentation as well as metadata that supports open science and emerging norms that facilitate software citation, computational reproducibility / frictionless reuse, and interoperability. Model authors can also request private peer review of their computational models. Models that pass peer review receive a DOI once published.
All users of models published in the library must cite model authors when they use and benefit from their code.
Please check out our model publishing tutorial and feel free to contact us if you have any questions or concerns about publishing your model(s) in the Computational Model Library.
We also maintain a curated database of over 7500 publications of agent-based and individual based models with detailed metadata on availability of code and bibliometric information on the landscape of ABM/IBM publications that we welcome you to explore.
Displaying 10 of 1101 results for "Clint A Penick" clear search
Auctionsimulation
Deniz Kayar | Published Wednesday, August 12, 2020This repository the multi-agent simulation software for the paper “Comparison of Competing Market Mechanisms with Reinforcement Learning in a CarPooling Scenario”. It’s a mutlithreaded Javaapplication.
Pedestrian Scramble
Sho Takami Rami Lake Dara Vancea | Published Tuesday, November 30, 2021 | Last modified Tuesday, June 10, 2025This is a model intended to demonstrate the function of scramble crossings and a more efficient flow of pedestrian traffic with the presence of diagonal crosswalks.
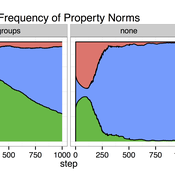
Cultural Group Selection of Sustainable Institutions
Timothy Waring Paul Smaldino Sandra H Goff | Published Wednesday, June 10, 2015 | Last modified Tuesday, August 04, 2015We develop a spatial, evolutionary model of the endogenous formation and dissolution of groups using a renewable common pool resource. We use this foundation to measure the evolutionary pressures at different organizational levels.
Hybrid traffic model
Patrick Taillandier Arnaud Banos Nathalie Corson | Published Thursday, March 16, 2017The model aims at simulating the car traffic. It allows to use either a macro or a micro sub-model for the simulation of the flow on the roads.
Ant Colony Optimization for infrastructure routing
Igor Nikolic Emile Chappin P W Heijnen | Published Wednesday, March 05, 2014 | Last modified Saturday, March 24, 2018The mode implements a variant of Ant Colony Optimization to explore routing on infrastructures through a landscape with forbidden zones, connecting multiple sinks to one source.
Peer reviewed The foraging potential of the Holocene Cape South Coast of South Africa without the Palaeo-Agulhas Plain
Marco Janssen Colin Wren | Published Monday, August 12, 2019The Palaeo-Agulhas Plain formed an important habitat exploited by Pleistocene hunter-gatherer populations during periods of lower sea level. This productive, grassy habitat would have supported numerous large-bodied ungulates accessible to a population of skilled hunters with the right hunting technology. It also provided a potentially rich location for plant food collection, and along its shores a coastline that moved with the rise and fall of sea levels. The rich archaeological and paleontological records of Pleistocene sites along the modern Cape south coast of South Africa, which would have overlooked the Palaeo-Agulhas Plain during Pleistocene times of lower sea level, provides a paleoarchive of this extinct ecosystem. In this paper, we present a first order illustration of the “palaeoscape modeling” approach advocated by Marean et al. (2015). We use a resourcescape model created from modern studies of habitat productivity without the Palaeo-Agulhas Plain. This is equivalent to predominant Holocene conditions. We then run an agent-based model of the human foraging system to investigate several research questions. Our agent-based approach uses the theoretical framework of optimal foraging theory to model human foraging decisions designed to optimize the net caloric gains within a complex landscape of spatially and temporally variable resources. We find that during the high sea-levels of MIS 5e (+5-6 m asl) and the Holocene, the absence of the Plain left a relatively poor food base supporting a much smaller population relying heavily on edible plant resources from the current Cape flora. Despite high species diversity of plants with edible storage organs, and marine invertebrates, encounter rates with highly profitable resources were low. We demonstrate that without the Palaeo-Agulhas Plain, human populations must have been small and low density, and exploited plant, mammal, and marine resources with relatively low caloric returns. The exposure and contraction of the Palaeo-Agulhas Plain was likely the single biggest driver of behavioral change during periods of climate change through the Pleistocene and into the transition to the Holocene.
Shellmound Mobility
Henrique de Sena Kozlowski | Published Saturday, June 15, 2024Least Cost Path (LCP) analysis is a recurrent theme in spatial archaeology. Based on a cost of movement image, the user can interpret how difficult it is to travel around in a landscape. This kind of analysis frequently uses GIS tools to assess different landscapes. This model incorporates some aspects of the LCP analysis based on GIS with the capabilities of agent-based modeling, such as the possibility to simulate random behavior when moving. In this model the agent will travel around the coastal landscape of Southern Brazil, assessing its path based on the different cost of travel through the patches. The agents represent shellmound builders (sambaquieiros), who will travel mainly through the use of canoes around the lagoons.
How it works?
When the simulation starts the hiker agent moves around the world, a representation of the lagoon landscape of the Santa Catarina state in Southern Brazil. The agent movement is based on the travel cost of each patch. This travel cost is taken from a cost surface raster created in ArcMap to represent the different cost of movement around the landscape. Each tick the agent will have a chance to select the best possible patch to move in its Field of View (FOV) that will take it towards its target destination. If it doesn’t select the best possible patch, it will randomly choose one of the patches to move in its FOV. The simulation stops when the hiker agent reaches the target destination. The elevation raster file and the cost surface map are based on a 1 Arc-second (30m) resolution SRTM image, scaled down 5 times. Each patch represents a square of 150m, with an area of 0,0225km². The dataset uses a UTM Sirgas 2000 22S projection system. There are four different cost functions available to use. They change the cost surface used by the hikers to navigate around the world.
Peer reviewed Modern Wage Dynamics
J M Applegate | Published Sunday, June 05, 2022The Modern Wage Dynamics Model is a generative model of coupled economic production and allocation systems. Each simulation describes a series of interactions between a single aggregate firm and a set of households through both labour and goods markets. The firm produces a representative consumption good using labour provided by the households, who in turn purchase these goods as desired using wages earned, thus the coupling.
Each model iteration the firm decides wage, price and labour hours requested. Given price and wage, households decide hours worked based on their utility function for leisure and consumption. A labour market construct chooses the minimum of hours required and aggregate hours supplied. The firm then uses these inputs to produce goods. Given the hours actually worked, the households decide actual consumption and a market chooses the minimum of goods supplied and aggregate demand. The firm uses information gained through observing market transactions about consumption demand to refine their conceptions of the population’s demand.
The purpose of this model is to explore the general behaviour of an economy with coupled production and allocation systems, as well as to explore the effects of various policies on wage and production, such as minimum wage, tax credits, unemployment benefits, and universal income.
…
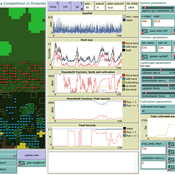
Peer reviewed LUCID: Land Use Competition In Drylands
Birgit Müller Gunnar Dressler Lance Robinson | Published Wednesday, April 12, 2023The Land Use Competition in Drylands (LUCID) model is a stylized agent-based model of a smallholder farming system. Its main purpose is to illustrate how competition between pastoralism and crop cultivation can affect livelihoods of households, specifically their food security. In particular, the model analyzes whether the expansion of crop cultivation may contribute to a vicious circle where an increase in cultivated area leads to higher grazing pressure on the remaining pastureland, which in turn may cause forage shortages and livestock loss for households which are then forced to further expand their cultivated area in order to increase their food security. The model does not attempt to replicate a particular case study but to generate a general understanding of mechanisms and drivers of such vicious circles and to identify possible scenarios under which such circles may be prevented.
The model is inspired by observations of the Borana land use system in Southern Ethiopia. The climatic and ecological conditions of the Borana zone favor pastoralism, and traditionally livelihoods have been based mainly on livestock keeping. Recent years, however, have seen an advancement of crop cultivation as a coping strategy, e.g., to compensate the loss of livestock, even though crop yields are low on average and successful harvests are infrequent.
In the model, it is possible to evaluate patterns of individual (single household) as well as overall (across all households) consumption and food security, depending on a range of ecological, climatic and management parameters.
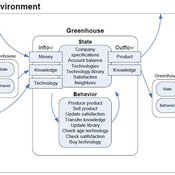
Universal Darwinism in Dutch Greenhouses
Julia Kasmire | Published Wednesday, May 09, 2012 | Last modified Saturday, April 27, 2013An ABM, derived from a case study and a series of surveys with greenhouse growers in the Westland, Netherlands. Experiments using this model showshow that the greenhouse horticulture industry displays diversity, adaptive complexity and an uneven distribution, which all suggest that the industry is an evolving system.
Displaying 10 of 1101 results for "Clint A Penick" clear search