About the CoMSES Model Library more info
Our mission is to help computational modelers develop, document, and share their computational models in accordance with community standards and good open science and software engineering practices. Model authors can publish their model source code in the Computational Model Library with narrative documentation as well as metadata that supports open science and emerging norms that facilitate software citation, computational reproducibility / frictionless reuse, and interoperability. Model authors can also request private peer review of their computational models. Models that pass peer review receive a DOI once published.
All users of models published in the library must cite model authors when they use and benefit from their code.
Please check out our model publishing tutorial and feel free to contact us if you have any questions or concerns about publishing your model(s) in the Computational Model Library.
We also maintain a curated database of over 7500 publications of agent-based and individual based models with detailed metadata on availability of code and bibliometric information on the landscape of ABM/IBM publications that we welcome you to explore.
Displaying 10 of 52 results for "Sylvia Helena Annuth" clear search
UK Demographic Simulator
Tony Lawson | Published Monday, February 27, 2012 | Last modified Tuesday, October 21, 2014A dynmaic microsimulation model to project the UK population over time
Agent-Based Simulation for International Tax Compliance
Peter Gerbrands | Published Tuesday, July 18, 2023Country-by-Country Reporting and Automatic Exchange of Information have recently been implemented in European Union (EU) countries. These international tax reforms increase tax compliance in the short term. In the long run, however, taxpayers will continue looking abroad to avoid taxation and, countries, looking for additional revenues, will provide opportunities. As a result, tax competition intensifies and the initial increase in compliance could reverse. To avoid international tax reforms being counteracted by tax competition, this paper suggests bilateral responsive regulation to maximize compliance. This implies that countries would use different tax policy instruments toward other countries, including tax and secrecy havens.
To assess the effectiveness of fully or partially enforce tax policies, this agent based model has been ran many times under different enforcement rules, which influence the perceived enforced- and voluntary compliance, as the slippery-slope model prescribes. Based on the dynamics of this perception and the extent to which agents influence each other, the annual amounts of tax evasion, tax avoidance and taxes paid are calculated over longer periods of time.
The agent-based simulation finds that a differentiated policy response could increase tax compliance by 6.54 percent, which translates into an annual increase of €105 billion in EU tax revenues on income, profits, and capital gains. Corporate income tax revenues in France, Spain, and the UK alone would already account for €35 billion.
Tyche
Tony Lawson | Published Tuesday, February 28, 2012 | Last modified Saturday, April 27, 2013Demographic microsimulation model used in speed tests against LIAM 2.
The tragedy of the park: an agent-based model on endogenous and exogenous institutions for the management of a forest.
Elena Vallino | Published Wednesday, March 27, 2013 | Last modified Thursday, April 26, 2018I model a forest and a community of loggers. Agents follow different kinds of rules in order to log. I compare the impact of endogenous and of exogenous institutions on the state of the forest and on the profit of the users, representing different scenarios of participatory conservation projects.
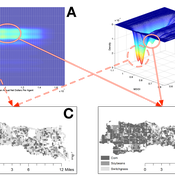
This model extends the original Artifical Anasazi (AA) model to include individual agents, who vary in age and sex, and are aggregated into households. This allows more realistic simulations of population dynamics within the Long House Valley of Arizona from AD 800 to 1350 than are possible in the original model. The parts of this model that are directly derived from the AA model are based on Janssen’s 1999 Netlogo implementation of the model; the code for all extensions and adaptations in the model described here (the Artificial Long House Valley (ALHV) model) have been written by the authors. The AA model included only ideal and homogeneous “individuals” who do not participate in the population processes (e.g., birth and death)–these processes were assumed to act on entire households only. The ALHV model incorporates actual individual agents and all demographic processes affect these individuals. Individuals are aggregated into households that participate in annual agricultural and demographic cycles. Thus, the ALHV model is a combination of individual processes (birth and death) and household-level processes (e.g., finding suitable agriculture plots).
As is the case for the AA model, the ALHV model makes use of detailed archaeological and paleoenvironmental data from the Long House Valley and the adjacent areas in Arizona. It also uses the same methods as the original model (from Janssen’s Netlogo implementation) to estimate annual maize productivity of various agricultural zones within the valley. These estimates are used to determine suitable locations for households and farms during each year of the simulation.
Stylized agricultural land-use model for resilience exploration
Patrick Bitterman | Published Tuesday, June 14, 2016 | Last modified Monday, April 08, 2019This model is a highly stylized land use model in the Clear Creek Watershed in Eastern Iowa, designed to illustrate the construction of stability landscapes within resilience theory.
Peer reviewed Theoretical Model of Oak Persistence Under Competition and Herbivory
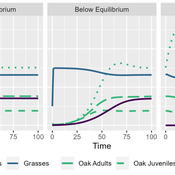
MV Eitzel Solera | Published Tuesday, October 25, 2022This model is intended to support oak tree management by representing the dynamics of oaks in multiple life stages and their competitors and consumers. This is implemented using a differential equation-based theoretical model representing three life stages of oaks: seedlings, juveniles, and adults. It includes the population dynamics of seedlings transitioning to juveniles, juveniles to adults, and adults producing new seedlings, as well as survival rates for each of the stages. It also includes a model of competition for light and water within seedlings and between seedlings and annual grasses. Finally, there is a predation term representing herbivores eating seedlings and grasses, using a Holling Type II (satiating) response with interference for predators and a death rate which depends on the resource extraction rate.
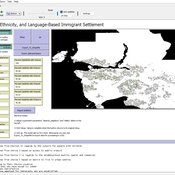
Geospatial Agent-Based Model of Immigrant Settlement Dynamics in Metro Vancouver
Liliana Perez Navid Mahdizadeh Gharakhanlou Maryam Yousefi | Published Wednesday, December 03, 2025This agent-based model simulates how new immigrant households choose where to live in Metro Vancouver under the origins diversity scenario. The model begins with 16,000 household agents, reflecting an expected annual population increase of about 42,500 people based on an average household size of 2.56. Each agent is assigned four characteristics: one of ten origin categories, income level (adjusted using NOC data and recent immigrant earnings), likelihood of having children, and preferred mode of commuting. The ten origin groups are drawn from Census patterns, including six subgroups within the broader Asian category (China, India, the Philippines, Iran, South Korea, and Other Asian countries) and two categories for immigrants from the Americas. This refined classification better captures the diversity of newcomers arriving in the region.
Peer reviewed AgModel
Isaac Ullah | Published Friday, December 06, 2024AgModel is an agent-based model of the forager-farmer transition. The model consists of a single software agent that, conceptually, can be thought of as a single hunter-gather community (i.e., a co-residential group that shares in subsistence activities and decision making). The agent has several characteristics, including a population of human foragers, intrinsic birth and death rates, an annual total energy need, and an available amount of foraging labor. The model assumes a central-place foraging strategy in a fixed territory for a two-resource economy: cereal grains and prey animals. The territory has a fixed number of patches, and a starting number of prey. While the model is not spatially explicit, it does assume some spatiality of resources by including search times.
Demographic and environmental components of the simulation occur and are updated at an annual temporal resolution, but foraging decisions are “event” based so that many such decisions will be made in each year. Thus, each new year, the foraging agent must undertake a series of optimal foraging decisions based on its current knowledge of the availability of cereals and prey animals. Other resources are not accounted for in the model directly, but can be assumed for by adjusting the total number of required annual energy intake that the foraging agent uses to calculate its cereal and prey animal foraging decisions. The agent proceeds to balance the net benefits of the chance of finding, processing, and consuming a prey animal, versus that of finding a cereal patch, and processing and consuming that cereal. These decisions continue until the annual kcal target is reached (balanced on the current human population). If the agent consumes all available resources in a given year, it may “starve”. Starvation will affect birth and death rates, as will foraging success, and so the population will increase or decrease according to a probabilistic function (perturbed by some stochasticity) and the agent’s foraging success or failure. The agent is also constrained by labor caps, set by the modeler at model initialization. If the agent expends its yearly budget of person-hours for hunting or foraging, then the agent can no longer do those activities that year, and it may starve.
Foragers choose to either expend their annual labor budget either hunting prey animals or harvesting cereal patches. If the agent chooses to harvest prey animals, they will expend energy searching for and processing prey animals. prey animals search times are density dependent, and the number of prey animals per encounter and handling times can be altered in the model parameterization (e.g. to increase the payoff per encounter). Prey animal populations are also subject to intrinsic birth and death rates with the addition of additional deaths caused by human predation. A small amount of prey animals may “migrate” into the territory each year. This prevents prey animals populations from complete decimation, but also may be used to model increased distances of logistic mobility (or, perhaps, even residential mobility within a larger territory).
…
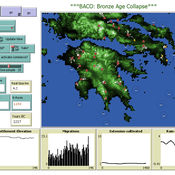
The Bronze Age Collapse model (BACO model)
Marco Vidal-Cordasco | Published Friday, October 09, 2020The Bronze Age Collapse model (BACO model) is written using free NetLogo software v.6.0.3. The purpose of using the BACO model is to develop a tool to identify and analyse the main factors that made the Late Bronze Age and Early Iron Age socio-ecological system resilient or vulnerable in the face of the environmental aridity recorded in the Aegean. The model explores the relationship between dependent and independent variables. Independent variables are: a) inter-annual rainfall variability for the Late Bronze Age and Early Iron Age in the eastern Mediterranean, b) intensity of raiding, c) percentage of marine, agricultural and other calorie sources included in the diet, d) soil erosion processes, e) farming assets, and d) storage capacity. Dependent variables are: a) human pressure for land, b) settlement patterns, c) number of commercial exchanges, d) demographic behaviour, and e) number of migrations.
Displaying 10 of 52 results for "Sylvia Helena Annuth" clear search