About the CoMSES Model Library more info
Our mission is to help computational modelers develop, document, and share their computational models in accordance with community standards and good open science and software engineering practices. Model authors can publish their model source code in the Computational Model Library with narrative documentation as well as metadata that supports open science and emerging norms that facilitate software citation, computational reproducibility / frictionless reuse, and interoperability. Model authors can also request private peer review of their computational models. Models that pass peer review receive a DOI once published.
All users of models published in the library must cite model authors when they use and benefit from their code.
Please check out our model publishing tutorial and feel free to contact us if you have any questions or concerns about publishing your model(s) in the Computational Model Library.
We also maintain a curated database of over 7500 publications of agent-based and individual based models with detailed metadata on availability of code and bibliometric information on the landscape of ABM/IBM publications that we welcome you to explore.
Displaying 10 of 42 results for "Michaela Starkey" clear search
Peer reviewed AgModel
Isaac Ullah | Published Friday, December 06, 2024AgModel is an agent-based model of the forager-farmer transition. The model consists of a single software agent that, conceptually, can be thought of as a single hunter-gather community (i.e., a co-residential group that shares in subsistence activities and decision making). The agent has several characteristics, including a population of human foragers, intrinsic birth and death rates, an annual total energy need, and an available amount of foraging labor. The model assumes a central-place foraging strategy in a fixed territory for a two-resource economy: cereal grains and prey animals. The territory has a fixed number of patches, and a starting number of prey. While the model is not spatially explicit, it does assume some spatiality of resources by including search times.
Demographic and environmental components of the simulation occur and are updated at an annual temporal resolution, but foraging decisions are “event” based so that many such decisions will be made in each year. Thus, each new year, the foraging agent must undertake a series of optimal foraging decisions based on its current knowledge of the availability of cereals and prey animals. Other resources are not accounted for in the model directly, but can be assumed for by adjusting the total number of required annual energy intake that the foraging agent uses to calculate its cereal and prey animal foraging decisions. The agent proceeds to balance the net benefits of the chance of finding, processing, and consuming a prey animal, versus that of finding a cereal patch, and processing and consuming that cereal. These decisions continue until the annual kcal target is reached (balanced on the current human population). If the agent consumes all available resources in a given year, it may “starve”. Starvation will affect birth and death rates, as will foraging success, and so the population will increase or decrease according to a probabilistic function (perturbed by some stochasticity) and the agent’s foraging success or failure. The agent is also constrained by labor caps, set by the modeler at model initialization. If the agent expends its yearly budget of person-hours for hunting or foraging, then the agent can no longer do those activities that year, and it may starve.
Foragers choose to either expend their annual labor budget either hunting prey animals or harvesting cereal patches. If the agent chooses to harvest prey animals, they will expend energy searching for and processing prey animals. prey animals search times are density dependent, and the number of prey animals per encounter and handling times can be altered in the model parameterization (e.g. to increase the payoff per encounter). Prey animal populations are also subject to intrinsic birth and death rates with the addition of additional deaths caused by human predation. A small amount of prey animals may “migrate” into the territory each year. This prevents prey animals populations from complete decimation, but also may be used to model increased distances of logistic mobility (or, perhaps, even residential mobility within a larger territory).
…
Confirmation Bias improves Performance in a Signal Detection Task and evolves in an Evolutionary Algorithm
Michael Vogrin | Published Monday, May 08, 2023Confirmation Bias is usually seen as a flaw of the human mind. However, in some tasks, it may also increase performance. Here, agents are confronted with a number of binary Signals (A, or B). They have a base detection rate, e.g. 50%, and after they detected one signal, they get biased towards this type of signal. This means, that they observe that kind of signal a bit better, and the other signal a bit worse. This is moderated by a variable called “bias_effect”, e.g. 10%. So an agent who detects A first, gets biased towards A and then improves its chance to detect A-signals by 10%. Thus, this agent detects A-Signals with the probability of 50%+10% = 60% and detects B-Signals with the probability of 50%-10% = 40%.
Given such a framework, agents that have the ability to be biased have better results in most of the scenarios.
Peer reviewed ABM to create populations with realistic Big Five Personality Trait Expressions
Michael Vogrin | Published Tuesday, May 30, 2023This model aims at creating agent populations that have “personalities”, as described by the Big Five Model of Personality. The expression of the Big Five in the agent population has the following properties, so that they resemble real life populations as closely as possible:
-The population mean of each trait is 0.5 on a scale from 0 to 1.
-The population-wide distribution of each trait approximates a normal distribution.
-The intercorrelations of the Big Five are close to those observed in the Literature.
The literature used to fit the model was a publication by Dimitri van der Linden, Jan te Nijenhuis, and Arnold B. Bakker:
…
Waste separation in small-world networks
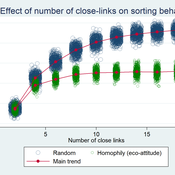
František Kalvas Michaela Kudrnáčová | Published Monday, September 30, 2019The model answers the question how homophily and number of close-links in small-world network influences behavior of consumats. The results show that the more close-links the more probable the consumat follows the major behavior, but homophilly blocks the major behavior and supports survival of the minor behavior.
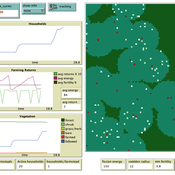
Swidden farming by individual households
C Michael Barton | Published Sunday, April 27, 2008 | Last modified Saturday, April 27, 2013Swidden Farming is designed to explore the dynamics of agricultural land management strategies.
Patch choice model from Optimal Foraging Theory (Human Behavioral Ecology)
C Michael Barton | Published Saturday, November 22, 2008 | Last modified Saturday, April 27, 2013NetLogo model of patch choice model from optimal foraging theory (human behavioral ecology).
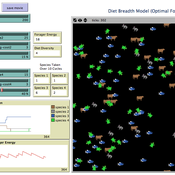
Diet breadth model from Optimal Foraging Theory (Human Behavioral Ecology)
C Michael Barton | Published Wednesday, November 26, 2008 | Last modified Thursday, March 12, 2015Diet breadth is a classic optimal foraging theory (OFT) model from human behavioral ecology (HBE). Different resources, ranked according to their food value and processing costs, are distributed in th
Hominin ecodynamics v.2
C Michael Barton | Published Monday, September 19, 2011 | Last modified Friday, March 28, 2014Simulates biobehavioral interactions between 2 populations of hominins.
Peer reviewed Hominin ecodynamics v.1
C Michael Barton | Published Saturday, October 01, 2011 | Last modified Friday, March 28, 2014Biobehavioral interactions between two populations under different movement strategies.
Hominin Ecodynamics v.1.1 (update for perception and interaction)
C Michael Barton | Published Wednesday, August 15, 2012 | Last modified Saturday, April 27, 2013Models land-use, perception, and biocultural interactions between two forager populations.
Displaying 10 of 42 results for "Michaela Starkey" clear search