Homophily-driven Network Evolution and Diffusion 1.0.0
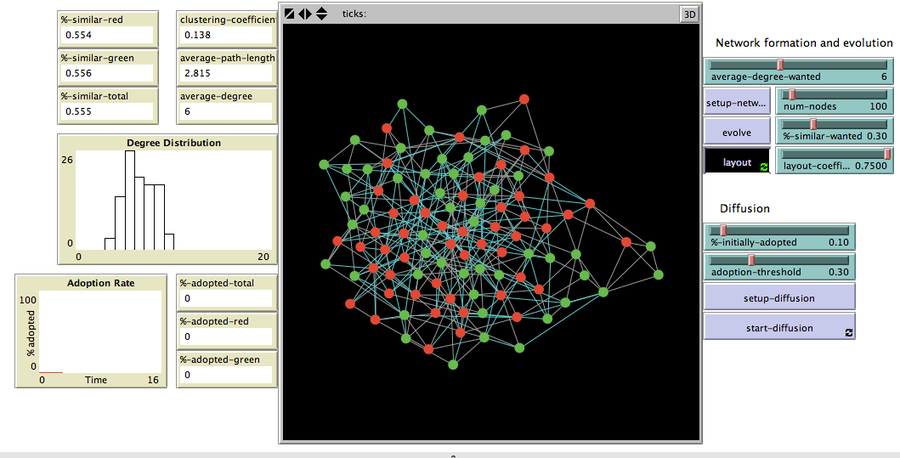
The two key processes included in the model are network evolution and diffusion. The evolution process of the homophilious network is inspired by the famous “Segregation Model” (Schelling 1971). The process starts with a small-world network (Watts 1999; Wilensky 2005). In our network, each agent has a threshold value for her “happiness level”. This level is related to the fraction of the friends with the same status in the agent’s network neighborhood, as in Schelling’s model. “Unhappy” agents (i.e. agents with fewer neighbors of their own status than what is desired according to the agent’s happiness threshold) form ties with agents alike, and break ties with others. %-similar-wanted is the model parameter that represents this personal threshold.
Homophily, besides its indirect role through shaping the network structure on which the diffusion takes place, also has a direct influence on the diffusion processes in the model via information flows. The network structure stays intact during the diffusion phase. In other words, we assume that the adopted behavior does not lead to homophilious tie formation or dissolution.
Diffusion starts with the initiation of the early adopters and takes off as people make decisions via social influence whether to adopt the innovation or not. The adoption mechanism in this study is an example of threshold models (Granovetter 1978). The most important factor in adoption decisions is the “adoption threshold”. An agent adopts the innovation if the number of same status friends in the network neighborhood who adopted the innovation is more than the “adoption threshold”. There are two ways of expressing the threshold, as an absolute number or as a fraction. Since our diffusion process includes making a decision about whether to adopt or not, expressing it as a fraction is preferred (Watts 2002).